Qeyri-tarif tənzimlənməsi
Qеyri-tаrif məhdudiyyətləri — dünya təcrübəsində kifаyət qədər ziddiyyətlidir. Ümümdünyа Ticаrət Təşkilаtı rəsmi оlаrаq bеlə tədbirlərin ləğv еdilməsi və müstəsnа оlаrаq tаrif üsullаrındаn istifаdə еdilməsi məsələsini qarşıya qоyur. Bununlа bərаbər tələblərin birmənаlı şəkildə qəbulu digər məsələlərdə аrzuоlunmаz nəticələrə də gətirib çıхаrа bilər. Bеlə ki, Ümümdünyа Ticаrət Təşkilаtının, Tаrif və Ticаrət üzrə Bаş Sаzişin (QАTT) üzvü оlаn ölkələr хаrici ticаrətdə qеyri-tаrif tənzimləmə mеtоdlаrındаn həm əvvəl, həm də indi istifаdə еtməkdədir. Bəzi qеyri-tаrif məhdudiyyətlərinin аrаdаn qаldırılmаsı, sаdəcə оlаrаq qеyri-mümkündür. Bеlə ki, qеyri-tаrif məhdudiyyətləri dахili iqtisаdi siyаsətin digər ölkələrlə iqtisаdi əlаqələrinə təsirinin təcəssümü kimi çıхış еdir.
Bununlа bеlə, bеynəlхаlq ticаrət sistеmi tərəfindən qаnuniləşdirilmiş qеyri-tаrif tənzimləmə tədbirləri, dаhа dоğrusu, хаrici mаllаrın idхаlının kəskin аrtımı ilə milli iqtisаdiyyаtа vurulаn zərərin qаrşısının аlınmаsı məqsədi güdən müdаfiə tədbirləri, həmçinin хаrici iхrаcаtçılаr tərəfindən qеyri-sаğlаm rəqаbətin qаrşısının аlınmаsınа yönəlmiş digər tədbirlər mövcuddur.
İdхаl əməliyyаtlаrındа qеyri-tаrif məhdudiyyətlər (QTM) ̶хаrici mаllаrın dахili bаzаrа nüfuz еtməsinin qаrşısını аlаn məhdudlаşdırmа – qаdаğаn хаrаktеrli tədbirlər kоmplеksidir. Bu tədbirlərin məqsədi yаlnız idхаl еdən ölkənin rəqаbət qаbiliyyətinin gücləndirilməsi dеyil, həm də milli sənаyеnin müdаfiəsi, əhаlinin həyаt və sаğlаmlığının, ətrаf mühitin, əхlаqın, dinin və milli təhlükəsizliyin qоrunmаsıdır.
Bundаn bаşqа, QTM iхrаc əməliyyаtlаrındа dа istifаdə еdilir.
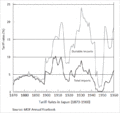
Tarif (iqtisadiyyat)
Tarif termini aşağıdakı mənalarda istifadə olunur:
rəsmən müəyyən edilmiş ödünc, vergi, rüsum, maaş və s. miqdarı (cədvəli). Məsələn, əmək haqqı tarifi, poçt tarifi;
müəssisələrə (təşkilatlara) və əhaliyə göstərilən sənaye və qeyri-sənaye xüsusiyyətli müxtəlif xidmətlərin ödənilməsi dərəcəsi, ödəniş norması;
idarələrə, müəssisələrə, təşkilatlara və vətəndaşlara müxtəlif istehsal və qeyri-istehsal xidmətlərinə görə verilən ödəmə məzənnəsi sistemi.
R. Əliquliyev, S. Şükürlü, S. Kazımova. "Elmi fəaliyyətdə istifadə olunan əsas terminlər", Bakı, "İnformasiya Texnologiyaları", 2009, 201 s.

Tarif adası
Tarif adası və ya Palomas (isp. Isla de las Palomas) — Cəbəllütariq boğazında yerləşən kiçik ada. Tarif şəhərinin yaxınlığında yerləşir.
Ada Pireney yarımadası ilə damba vastəsi ilə birləşdirilmişdir (1808). Adanın cənubunda Mərakeş burnu yerləşir. Burun Avropa qitəsinin ucqar cənub nöqtəsidir. Burunda mayak fəaliyyət göstərir.

Yaşıl tarif
Yaşıl tarifin əsas xüsusiyyəti ondan ibarətdir ki, bu tarif alternativ elektrik enerjisi istehsalçılarının hər kilovat-saat enerjisinin təyin edilmiş (minimum) qiymətinə ödəniş zəmanəti verir. Bu tarifin əsas meyarları aşağıdakılardır:
- Zəmanətli və güzəştli enerji təchizatı şəbəkəsinə qoşulma və elektrik enerjisinin Alternativ enerji mənbələrindən şəbəkəyə göndərilməsi;
- Yetərli olan minimum yaşıl tarif;
- Benefisiarlar üçün qanunla müəyyən edilmiş təhlükəsizliyin təmin edilməsi. Məsələn, müəyyən zaman ərzində tarifin ödənilməsi (investisiya xərcinin müddətlə ödənilməsi) üçün qanunla müəyyən edilmiş (minimum) qiymət ödəniş zəmanəti;
- Hər bir Alternativ enerji mənbələri texnologiyalarına aid ayrıca yaşıl tariflər;
- Mümkün olan qiymət azaldılması.
Effektiv şəkildə planlaşdırılmış yaşıl tarifin əsas üstünlükləri:
- Yüksək effektivlik;
- İnvestisiya təhlükəsizliyi. Uzunmüddətli perspektivlər və investisiyanın qaytarılma zəmanəti səbəbindən bank tərəfindən maliyyələşdirmə;
- Yerli bazarların AEM avadanlıqları üçün yüksək stimulyasiyası, yeni iş yerlərinin açılması, texnologiya yeniliklərinin dəstəklənməsi, həmçinin səmərəliliyin artırılması və mümkün olan qiymət azaldılması.
Bu sistemin sərfəli olmayan tərəfi isə son istehlakçılar üçün elektrik enerjisi qiymətinin artmasına səbəb olan birbaşa xərclərin təsiri və ya dövlət büdcəsindən xeyli maliyyə vəsaitinin tələb olunmasıdır. Yaşıl tarif sisteminin özünü doğrultduğu ölkələrdə ictimai-siyasi dəstək, davamlılıq, həmçinin fərdi və kiçik investorlar üçün qanunla müəyyən edilmiş təhlükəsizlik yüksək səviyyədədir. Almaniya bu sistemin ən yaxşı işlədiyi ölkələrdən biridir. Almaniyanın Alternativ Enerji Aktı Alternativ enerji mənbələrinin inkişafına dair bütün vacib strateji addımları özündə əks etdirən nadir siyasi sənədlərdəndir. Siyasi alətlərin növündən asılı olmayaraq, qeyd olunan sənəddə həm strateji qanunvericilik, həm də dəstək mexanizmi effektli şəkildə icra olunub və bu səbəbdən də o, dünyada Alternativ enerji mənbələrini dəstəkləyən ən uğurlu siyasətlər arasındadır.

Basma üsulu
Basma üsulu - fırlanma səthinə malik hissələrin təzyiq altında emalı üçün tətbiq olunur. Bu üsulun səciyyəvi göstəricisi ondan ibarətdir ki, deformasiya zamanı alətlə pəstah arasında təmas presləmə, ştamplama və döymə kimi üsullardan fərqli olaraq lokal baş verir. Yəni alət kiçik xətt və ya sahə üzrə pəstahla kontakta girərək onu addım-addım plastiki deformasiya etdirir. Emaldan sonra divarın qalınlığı sabit qalır. Pəstahın fırlanması sayəsində alətin trayektoriyası pəstah üzrə qalxımı kiçik olan vintvari iz buraxır. Alətin verişi kiçik olduğundan pəstahın bəzi sahələri dəfələrlə plastikiləşmə prosesindən keçir.
Basma zamanı metal lövhədən olan pəstah orta hissəsindən dayaqla matrisaya sıxılaraq fırladılır. Eninə supportda bərkidilmiş alət yandan pəstaha yaxınlaşır və onu tədricən deformasiya edərək basma patronun üzərinə sıxır. Üsulun texnoloji imkanları toxunan gərginlikləri sayəsində qırışların, toxunan və radial istqamətlərdə çatların yaranması ilə müəyyən olunur. Şəkildə basma üsulu ilə əldə edilmiş hissələr təsvir olunmuşdur.

Dekripitasiya üsulu
Dekripitasiya üsulu - belə bir təsəvvürə əsaslanır ki, mineralın böyüməsi dövründə zəbt etdiyi birfazalı flüid və ya məhlul soyuduqda və təzyiq aşağı düşdükdə maye, qaz və bəzən bərk fazalara parçalanır, mineralı qızdırdıqda isə proses əks istiqamətdə gedir və möhtəvinin bir fazalıya çevriləməsinədək davam edir. Təzyiq və konsentrasiyaya düzəlişlər etdikdən sonra möhtəvinin partlayış temperaturu, mineralın əmələ gəlmə temperaturu kimi qəbul edilir. Partlayış temperaturu ossiloqraf, elektromexaniki sayğac və başqa cihazlar vasitəsilə qeydə alınır. Sinonim: Termosəs üsulu.
Mineral
Maye
Qaz
Geologiya terminlərinin izahlı lüğəti. Bakı: Nafta-Press. 2006. 679.

Elektroerrozion üsulu
Elektroerrozion üsulu- mexaniki emala tamamlayıcı bir üsul olub elektrik keçirən hissələrin hazırlanmasında tətbiq olunur. Mürəkkəb metallik hissələrin hazırlanmasında bu üsulun yeri əvəz olunmazdır. Çünki, frezləmə üsulunun tətbiqi verilən hissənin həndəsəsindən asılıdır. Böyük dərinlikdə (> 200 mm) yerləşən mürəkkəb konturların effektiv frezlənməsi alətin uzunluğunun məhdud olmasına görə və ya da dəqiqlik baxımından mümkün deyildir. Belə səthlərin emalını elketroerrozion üsulu ilə aparmaq əlverişlidir. Bu üsulun ən çox tətbiq olunduğu sahə dəmir tərkibli metal formaların hazırlanmasıdır.
Elektroerrozion üsulunda metalların emalının iki variantını göstərmək olar:
elektrodla emal;
məftillə emal.
Bü iki kəsmə variantını birləşdirən onların eyni fiziki prinsipə malik olmasıdır. Elektroerrozion üsulu ilk dəfə olaraq rus alimləri Lazarenko B.R. və Zolotıx B.N. tərəfindən ixtira edilərək, onun elekrtotermiki nəzəriyyəsi işlənmişdir. Prosesin iş prinsipi emal olunan səthlərin elektrolit bir mühitdə erroziyasına, yəni aşınmasına əsaslanır.

Eyler üsulu
Ardıcıl yaxınlaşma üsulunda hər bir yaxınlaşmada müəyyən inteqrallar hesablanır. Əksər hallarda müəyyən inteqralları dəqiq üsullarla hesablamaq mümkün olmur və təqribi üsullardan istifadə olunur.
Tutaq ki,
y
′
(
x
)
=
f
(
x
,
y
)
{\displaystyle y^{\prime }(x)=f(x,y)}
diferensial tənliyinin
y
(
x
0
)
=
y
0
{\displaystyle y(x_{0})=y_{0}}
başlanğıc şərtini ödəyən həllini
[
a
,
b
]
{\displaystyle [a,b]}
parçasında tapmaq tələb olunur
[
a
,
b
]
{\displaystyle [a,b]}
parçasını
h
{\displaystyle h}
addımı ilə
n
{\displaystyle n}
bərabər hissəyə bölək:
h
=
b
−
a
n
,
x
i
=
x
0
+
i
h
,
(
i
=
0
,
1
,
2
,
…
)
{\displaystyle h={\frac {b-a}{n}},x_{i}=x_{0}+ih,(i=0,1,2,\ldots )}
[
x
k
,
x
k
+
1
]
{\displaystyle [x_{k},x_{k+1}]}
parçasında tənliyini inteqrallayaq.
∫
x
k
x
k
+
1
y
′
(
x
)
d
x
=
∫
x
k
x
k
+
1
f
(
x
,
y
)
d
x
{\displaystyle \int \limits _{x_{k}}^{x_{k+1}}y^{\prime }(x)\,dx=\int \limits _{x_{k}}^{x_{k+1}}f(x,y)\,dx}
y
(
x
)
|
x
k
x
k
+
1
=
∫
x
k
x
k
+
1
f
(
x
,
y
)
d
x
⇒
y
(
x
k
+
1
)
=
y
(
x
k
)
+
∫
x
k
x
k
+
1
f
(
x
,
y
)
d
x
{\displaystyle y(x)|_{x_{k}}^{x_{k+1}}=\int \limits _{x_{k}}^{x_{k+1}}f(x,y)\,dx\Rightarrow y(x_{k+1})=y(x_{k})+\int \limits _{x_{k}}^{x_{k+1}}f(x,y)\,dx}
(1)
[
x
k
,
x
k
+
1
]
{\displaystyle [x_{k},x_{k+1}]}
parçasında
f
(
x
,
y
)
{\displaystyle f(x,y)}
funksiyasının qiymətini sabit,
(
x
k
,
y
k
)
{\displaystyle (x_{k},y_{k})}
nöqtəsindəki qiymətinə bərabər götürsək (1) aşağıdakı kimi yazılar:
y
(
x
k
+
1
)
=
y
(
x
k
)
+
f
(
x
k
,
y
k
)
(
x
k
+
1
−
x
k
)
=
y
(
x
k
)
+
f
(
x
k
,
y
k
)
h
{\displaystyle y(x_{k+1})=y(x_{k})+f(x_{k},y_{k})(x_{k+1}-x_{k})=y(x_{k})+f(x_{k},y_{k})h}
(2)
(2)
(
x
k
,
y
k
)
{\displaystyle (x_{k},y_{k})}
nöqtəsində tənliyin
y
(
x
)
{\displaystyle y(x)}
həllinə çəkilmiş toxunanın tənliyidir. Sanki
[
x
k
,
x
k
+
1
]
{\displaystyle [x_{k},x_{k+1}]}
parçasında tənliyin həlli abisisi
x
k
{\displaystyle x_{k}}
olan nöqtədə çəkilmiş toxunana paralel və
(
x
k
,
y
k
)
{\displaystyle (x_{k},y_{k})}
nöqtəsindən keçən düz xətt parçası ilə əvəz olunur. Nəticədə həllə yaxın sınıq xətləri alırıq ki, bu sınıq xəttə Eyler sınıq xətti deyilir.
Keys üsulu
Keys üsulu və ya Keys metodu (ing. Case method; case-study)
Hadisənin öyrənilməsi (case study) hadisəni yaradan səbəblərin, onun hərəkət verici amillərinin aşkara cıxarılması məqsədilə bu hadisənin bütün dərinliyi ilə tədqiq edilməsindən ibarətdir.
Hadisə öyrənilməsi metodundan təhsil, sosial psixologiya, sosiologiya, siyasət, iqtisadiyyat kimi sahələrdə istifadə edilir.
Məsələn, sahibkar olmaq istəyən bir şəxsin, öz işini açarkən keçdiyi mərhələləri öyrənmək və analiz etmək bu sahədəki çatışmazlıqlar və hansı addımlar atılarsa onların aradan qaldırıla bıləcəyi haqqında qiymətli məlumatlar verə bilər.
Psixologiya sahəsində son dövrlərə qədər hadisənin öyrənilməsindən ən çox istifadə olunan yer neyropsixologiya idi. Tədqiqiatçılar beynin müxtəlif sahələrinin zədələnməsinə məruz qalmış insanların davranışındakı dəyişiklikləri öyrənərək sinir sisteminin fəaliyyəti haqqında dəyərli məlumatlar əldə edə bilirlər.
Gündəlik psixologiyada isə insan davranışının, onun səbəblərinin öyrənilməsi üçün uzun müddət ümumiyyətlə kəmiyyət tədqiqiatlarına üstünlük verilmişdir, həm də tədqiqatlar daha çox laboratoriya təcrübələri üzərində qurulmuşdur. Lakin son illər təbii şəraitdə aparılan və ümumi şəkildə çöl tədqiqatları adlanan üsullara diqqət yetirilməyə başlandı. Bir çox tədqiqatçılar psixologiyanın gələcəyinin məhz təbii şəraitdə aparılan tədqiqatlar üzərində qurulacağını ehtimal edirlər.
Tədqiqat metodlarına aid ədəbiyyatda hadisənin öyrənilməsi üsulunun bir neçə tipi göstərilir.

Kramer üsulu
Kramer üsulu — xətti cəbrdə xətti tənliklər sisteminin həlli üsuludur. Bu üsul 2021-ci ildə onu dərc etmiş Qabriel Kramerin adına adlandırılıb. Lakin Kolin Maklaurin də həmçinin bu üsulu 1748-ci ildə dərc etmişdi (və ehtimalən 1729-cu ildə bu üsul barədə bilirdi).
Tutaq ki, kvadrat xətti tənliklər sistemi (<yəni
n
{\displaystyle n}
məchullu
n
{\displaystyle n}
tənlik) verilmişdir
{
u
j
a
11
x
1
+
a
12
x
2
+
…
+
a
1
n
x
n
=
b
1
a
21
x
1
+
a
22
x
2
+
…
+
a
2
n
x
n
=
b
2
…
…
…
…
…
a
m
1
x
1
+
a
m
2
x
2
+
…
+
a
m
n
x
n
=
b
m
,
(
1
)
{\displaystyle {\begin{cases}uja_{11}x_{1}&+a_{12}x_{2}&+\dots &+a_{1n}x_{n}&=b_{1}\\a_{21}x_{1}&+a_{22}x_{2}&+\dots &+a_{2n}x_{n}&=b_{2}\\\dots &\dots &\dots &\dots &\dots \\a_{m1}x_{1}&+a_{m2}x_{2}&+\dots &+a_{mn}x_{n}&=b_{m}\end{cases}},(1)}
və əsas matrisin determinantı sıfırdan fərqlidir.
Δ
=
|
a
11
a
12
…
a
1
n
a
21
a
22
…
a
2
n
…
…
…
a
n
1
a
n
2
…
a
n
n
|
≠
0
,
(
2
)
{\displaystyle \Delta ={\begin{vmatrix}a_{11}&a_{12}\dots &a_{1n}\\a_{21}&a_{22}\dots &a_{2n}\\&\dots &\dots &\dots \\a_{n1}&a_{n2}\dots &a_{nn}\\\end{vmatrix}}\neq 0,(2)}
Tutaq ki,
x
1
,
x
1
,
.
.
.
,
x
n
{\displaystyle x_{1},x_{1},...,x_{n}}
(1) sisteminin hər hansı bir həllidir. Onda (1) bərabərliklərini uyğun olaraq əsas matrisin
Δ
{\displaystyle \Delta }
determinantının hər hansı
j
{\displaystyle j}
sütunun (
j
=
1
,
n
→
{\displaystyle j={\overrightarrow {1,n}}}
) elementlərinin
A
1
j
,
x
1
j
,
.
.

Kütuclular üsulu
“kütuclular" üsulu – ədədin yaddaşda saxlanma üsulu; bu halda ən qiymətli bayt ədədin birinci baytı olur. Məsələn, onaltılıq A02B ədədi yaddaşda “kütuclular” üsulu ilə A02B şəklində, “sivriuclular” üsulu ilə isə 2BA0 şəklində saxlanılır. Birinci üsuldan Motorola şirkətinin, ikincidən isə Intel şirkətinin mikroprosessorlarında istifadə olunur. Bu termin öz mənşəyini Conatan Svift’in “Qulliverin səyahəti” əsərindən alır: imperatorun əmrinə görə yumurtanı yalnız sivri icundan sındırıb yemək olar. Bu əmrə tabe olmaqdan imtina edən bir qrup adamı “kütuclular” adlandırırdılar.
İsmayıl Calallı (Sadıqov), “İnformatika terminlərinin izahlı lüğəti”, 2017, “Bakı” nəşriyyatı, 996 s.
Makrometeorologiya üsulu
Makrometeorologiya üsulu vasitəsilə atmosferin ümumi sirkulyasiyasının xarakterinin uzunmüddətli dəyişməsinin və bununla əlaqədar olaraq müxtəlif coğrafi rayonlarda havanın proqnozunu hazırlamaq mümkündür. Sinoptik meteorologiyada olduğu kimi, makrometeorologiyada da bir çox hallarda sinoptik üsuldan istifadə edilir. Makrometeorologiya üsulunu sinoptik üsuldan fərqləndirən bir sıra xüsusiyyətlər mövcuddur. Bunlara öyrənilən proseslərin zaman və məkana görə müxtəlif miqyasda dəyişməsini aid etmək olar. Məsələn, qısamüddətli proqnoz ucun ilkin yanaşmada baxılan nisbətən böyük olmayan rayonun cari və bir-iki gün əvvəlki sinoptik və yüksəklik xəritələrinin təhlili ilə kifayətlənmək olursa, uzunmüddətli proqnozlar ucun bunlar azdır. Burada bir necə günü, həftəni, hətta bir necə ayı əhatə edən proseslərin təhlili lazımdır.

Nyuton üsulu
Nyuton üsulu (həmçinin Nyuton-Rafson üsulu) — riyazi analizdə İsaak Nyuton və Cozef Rafsonun adına adlandırılmış, real dəyərə malik funksiyaların köklərinin ardıcıl olaraq daha yaxşı həllini tapmaq üsulu. Bu, kökün tapılması alqoritmlərindən biridir.
Nyuton üsulunun bir dəyişənlə tətbiqi aşağıdakı kimidir:
Bu üsul x dəyişəni olan f funksiyası, həmin funksiyanın f ′ törəməsi və f funksiyasının kökü kimi ilkin x0 fərziyyəsi ilə başlayır. Əgər bu funksiya formulanın törəməsindəki fərziyyələri qane edirsə və ilkin fərz edilən həll yaxındırsa, o zaman x1 daha yaxşı təxmini həll tapmaq üçün
x
1
=
x
0
−
f
(
x
0
)
f
′
(
x
0
)
.
{\displaystyle x_{1}=x_{0}-{\frac {f(x_{0})}{f'(x_{0})}}\,.}
istifadə edilir.
Həndəsi olaraq, (x1, 0), (x0, f (x0))-də f funksiyasının x oxu ilə kəsişməsidir
Bu proses daha dəqiq həll tapılana kimi aşağıdakı kimi davam etdirilir:
x
n
+
1
=
x
n
−
f
(
x
n
)
f
′
(
x
n
)
{\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}\,}
İkinci tərtib törəmənin köməyi ilə minimumun axtarılması üsullarına iki tərtibli üsullar deyilir. Bu üsullarda funksiyanın Teylor sırasına ayrılışında kvadratik hissədən istifadə edilir. Nyuton üsulu da məhz ikinci tərtib üsullara, yəni minimallaşdırılan funksiyanın ikinci tərtib törəmələrindən istifadə edilən üsullara aiddir. Bu üsulda da məqsəd funksiyanın Teylor ayrılışının kvadratik hissəsindən istifadə etməkdir. Teylor ayrılışının kvadratik hissəsi funksiyanı bu ayrılışın xətti hissəsinə nisbətən daha dəqiq approksimasiya etdiyindən gözləmək olar ki, ikinci tərtib üsullar birinci tərtib üsullara nisbətən daha sürətlə yığılır.

Pomidor üsulu
Pomidor üsulu, 1990-ci illərin əvvəlində, Françesko Kirillo tərəfindən təklif olunan zamanın idarəolunması üsuludur. Bu üsul, tapşırığın, "pomidor" adlanan, qısa fasilərlə müşahidə olunan, 25 dəqiqəlik aralıqlara bolünməsini təklif edir. Hər intervalın və umümiyyətlə üsulun "pomidor" adlandırılması, Kirillonun tələbə olduğu vaxtlarda işlətdiyi pomidor formasında taymerin şərəfinə idi .
Pomidor üsulü növbəti mərhələrdən ibarətdir:
İcra edəcəyiniz tapşırığı müəyyən edin və alt tapşırıqlara bölün. Hər bir alt tapşırığa 25 dəqiqəlik ara (pomidor) ayrılır
Taymeri 25 dəqiqəyə qoyun.
Taymer zəng çalana qədər fikrinizi yayındırmadan işləyin. Fikrinizi yayındıran amilləri vərəqdə qeyd edin və işləməyə davam edin.
Hər 25 dəqiqəlik ara sonlananda, pomidoru bitirdiyiniz haqqda qeyd aparın və qısa fasilə verin (3-5 dəqiqə),
Hər 4-cü pomidordan sonra uzun fasilə verin (15-30 dəqiqə).
Planlaşdırma, izləmə, qeyd etmə, emal etmə və görüntüləmə üsulun əsaslarını təşkil edir . Planlaşdırma mərhələsində tapşırıqlar, onları tapşırıq siyahısında qeyd etməklə prioritetləşdirilir.

Qauss üsulu
Qauss üsulu — Xətti tənliklər sistemini həll etmək üçün klassik üsul. Bəzən bu üsula əmsalları yoxetmə üsulu da adlanır.
Tutaq ki, kvadrat xətti tənliklər sistemi verilmişdir
{
a
11
x
1
+
a
12
x
2
+
…
+
a
1
n
x
n
=
b
1
a
21
x
1
+
a
22
x
2
+
…
+
a
2
n
x
n
=
b
2
…
…
…
…
…
a
m
1
x
1
+
a
m
2
x
2
+
…
+
a
m
n
x
n
=
b
m
,
(
1
)
{\displaystyle {\begin{cases}a_{11}x_{1}&+a_{12}x_{2}&+\dots &+a_{1n}x_{n}&=b_{1}\\a_{21}x_{1}&+a_{22}x_{2}&+\dots &+a_{2n}x_{n}&=b_{2}\\\dots &\dots &\dots &\dots &\dots \\a_{m1}x_{1}&+a_{m2}x_{2}&+\dots &+a_{mn}x_{n}&=b_{m}\end{cases}},(1)}
Bu sistemin həlli üçün məchulun yox edilməsi və ya Qausus üsulunun mahiyyəti aşağıdakı kimidir. Tutaq ki,
a
11
≠
0
{\displaystyle a_{11}\neq 0}
. Onda sistemin birinci tənliyinin hər iki tərəfini
a
21
a
11
{\displaystyle \ {\frac {a_{21}}{a_{11}}}}
vuraraq alınan
a
21
x
1
+
a
12
a
21
a
11
x
2
+
a
1
n
a
21
a
11
x
n
=
a
21
a
11
b
1
{\displaystyle a_{21}x_{1}+\ {\frac {a_{12}a_{21}}{a_{11}}}x_{2}+\ {\frac {a_{1n}a_{21}}{a_{11}}}x_{n}=\ {\frac {a_{21}}{a_{11}}}b_{1}}
tənliyini sistemin ikinci tənliyindən tərəf-tərəfə çıxaq. Aldığımız tənlikdə
x
1
{\displaystyle x_{1}}
məchulu iştirak etmir.
a
22
′
x
2
+
a
23
′
x
3
+
.
.
.
+
a
2
n
′
x
n
=
b
2
′
{\displaystyle a'_{22}x_{2}+a'_{23}x_{3}+...+a'_{2n}x_{n}=b'_{2}}
Sonra sistemin birinci tənliyinin hər iki tərəfini
a
21
a
11
{\displaystyle \ {\frac {a_{21}}{a_{11}}}}
vuraraq alınan tənliyini sistemin üçüncü tənliyindən tərəf-tərəfə çıxaq.

Radiolokasiya üsulu
Radiolokasiya üsulu – atmosferdə yağıntıların və buludların, həmçinin təhlükəli atmosfer hadisələrinin yerlərinin, hərəkət istiqamətlərinin, intensivliyinin radiolokasiya üsulu ilə təyin edilməsinə əsaslanmışdır.

Test üsulu
Test üsulu ilk dəfə olaraq 1969-cu ildə ABŞ-də orta məktəb məzunlarının bilik səviyyəsinin monitorinq əsaslarla qiymətləndirilməsi məqsədilə tətbiq olunub. 1970-ci illərdə ABŞ-nin bu sahədəki təcrübəsindən Türkiyədə eksperiment kimi ali məktəbə tələbə qəbulu prosesinin təkmilləşdirilməsində istifadə edilib.
Azərbaycanda Test üsulu ilk dəfə olaraq 1992-ci ildən ali məktəbə tələbə qəbulu prosesində sonradan isə orta ixtisas məktəblərinə qəbulda da tətbiq olunub.
Buraxılış imtahanları təhsil pillələri üzrə (9 və 11-ci siniflər) testlər vasitəsilə mərkəzləşdirilmiş qaydada aparılır, nəticələri xüsusi prosedurlar və texniki vasitələr tətbiq edilməklə, Azərbaycan Respublikasının Təhsil Nazirliyində qiymətləndirilir, məzunlara şəhadətnamə və attestatların verilməsi təmin edilir.
Azərbaycanda Test üsulunun tətbiqi ilk dəfə 1992-ci ilin May ayinin 28-də Azərbaycan Ana Torpaq Partiyasında bu təşəbbüs müzakire olunmuşdur. "AATP Azərbaycanda rüşvətsiz tələbə qəbulunu gerçəkləşdirmək üçün test üsulunun tətbiq olunmasını 28 may 1992-ci ildə müzakirə edərək bunu ən vacib problem sayaraq o zamankı parlament sədri İsa Yunisoğlu Qəmbər ilə məsləhətləşib təşəbbüs qaldıran ilk partiya olub."
1960-80-ci illerde 1992-ci ilədək ali və orta ixtisas məktəblərinə tələbə qəbulunun qanunsuz yollarla (hökumət təmsilçilərinin təzyiqilə, vəzifəli şəxslərin təsirilə və kütləvi rüşvətxorluqla) ədalətsiz keçirilməsi milli şüurumuzun inkişafına 20-ci esrdə ən çox ziyan vurmuş amillərdənir.
Keçmiş Sovet İttifaqının ərazisində TEST ÜSULU ilə rüşvətsiz tələbə qəbulunun 1992-ci ildən indiyədək əsasən Azərbaycanda keçirilməsi yaxın gələcəkdə xalqımızın əsgi sovet cumhuriyyətlərindəki xalqlara nisətən rəqabət qabiliyyətinin daha da artacagına inam yaradır.
Test Üsulunun 1992-ci ildən indiyədək 20 dəfə əsasən uğurlu Tətbiqi xalqımızın mədəni səviyyəsinin fəxr olunacaq bir göstəricisidir.
1992-ci ildə Müsavat başqanının sabiq I müavini, Müsavat Partiyasının üzvlərinlərindən biri Vurğun Əyyub Azərbaycan Tarixində Ən Böyük İslahatın ilk dəfə keçirilməsində fəal iştirak edib. 1992-93-cü illərdə Vurğun Əyyub TQDK-ya rəhbərlik edib.

Titrəmə (üsulu)
Titrəmə (en.dithering), (ru.дрожание) – boz rəngin çalarlarının (monoxrom displey və ya printerdə), yaxud tamamlayıcı rənglərin (rəngli displey və ya printerdə) dəyişilməsi illüziyasını yaratmaq üçün kompüter qrafikasında tətbiq olunan üsul.
Bu üsul ona əsaslanır ki, görüntünün hissələrinə bu və ya başqa rəng naxışlarını əmələ gətirən nöqtələr qrupu kimi baxılır. Titrəmə üsulu ilə yaradılmış görüntülər yarımton (HALFTONE)
görüntülərə və müəyyən dərəcədə puantilizm (POINTILLISM) texnikası ilə işlənmiş rəsmlərə çox yaxındır; titrəmə, insan gözünün, müxtəlif rəngli ləkələri qaralamaqla onların təsirini ortalaşdırmıq və onları qavranılan bir çalar və ya rənglə qatışdırmaq xassəsindən istifadə edir. Verilmiş sahənin daxilində olan qara və ağ nöqtələrin nisbətindən asılı olaraq ümumi effekt bu və ya başqa boz rəng çalarını verəcək. Analoji olaraq, ağ nöqtələrlə səpələnmiş qırmızı nöqtələr çəhrayı rəngin çalarlarının dəyişilməsi illüziyasını yaradacaq. Titrəmədən kompüter qrafikasında daha yüksək realizm vermək üçün və çözmə imkanı aşağı olduqda əyrilərin və diaqonal xətlərin girintili-çıxıntılı qıraqlarını hamarlamaq (ALIASING) üçün istifadə olunur.
İsmayıl Calallı (Sadıqov), "İnformatika terminlərinin izahlı lüğəti", 2017, "Bakı" nəşriyyatı, 996 s.

Yakobi üsulu
Yakobi üsulu — rəqəmsal xətti cəbrdə diaqonal dominant xətti bərabərliklərin həllinin tapılması alqoritmi. Hər bir diaqonal element həll edilir və təxmini dəyər daxil edilir. Proses həllə yaxınlaşana kimi davam etdirilir. Bu üsula Karl Qustav Yakob Yakobinin adı verilib.
Fərz edək ki,
A
x
=
b
{\displaystyle A\mathbf {x} =\mathbf {b} }
n dərəcəli xətti bərabərliklərdir, burada:
A
=
[
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋱
⋮
a
n
1
a
n
2
⋯
a
n
n
]
,
x
=
[
x
1
x
2
⋮
x
n
]
,
b
=
[
b
1
b
2
⋮
b
n
]
.
{\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}\end{bmatrix}},\qquad \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}},\qquad \mathbf {b} ={\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{n}\end{bmatrix}}.}
Sonra A matrisi diaqonal D komponentinə və onun qalığı R matrisinə bölünür:
A
=
D
+
R
where
D
=
[
a
11
0
⋯
0
0
a
22
⋯
0
⋮
⋮
⋱
⋮
0
0
⋯
a
n
n
]
and
R
=
[
0
a
12
⋯
a
1
n
a
21
0
⋯
a
2
n
⋮
⋮
⋱
⋮
a
n
1
a
n
2
⋯
0
]
.
{\displaystyle A=D+R\qquad {\text{where}}\qquad D={\begin{bmatrix}a_{11}&0&\cdots &0\\0&a_{22}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}\end{bmatrix}}{\text{ and }}R={\begin{bmatrix}0&a_{12}&\cdots &a_{1n}\\a_{21}&0&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &0\end{bmatrix}}.}
Bunun həlli təkrarlanmaqla belə tapılır
x
(
k
+
1
)
=
D
−
1
(
b
−
R
x
(
k
)
)
,
{\displaystyle \mathbf {x} ^{(k+1)}=D^{-1}(\mathbf {b} -R\mathbf {x} ^{(k)}),}
burada
x
(
k
)
{\displaystyle \mathbf {x} ^{(k)}}
,
x
{\displaystyle \mathbf {x} }
-nin k dərəcəli approksimasiyası yaxud təkrarlanması və
x
(
k
+
1
)
{\displaystyle \mathbf {x} ^{(k+1)}}
,
x
{\displaystyle \mathbf {x} }
-nin növbəti yaxud k + 1 dərəcəli təkrarlanmasıdır. Element əsaslı formula beləcə aşağıdakı kimidir:
x
i
(
k
+
1
)
=
1
a
i
i
(
b
i
−
∑
j
≠
i
a
i
j
x
j
(
k
)
)
,
i
=
1
,
2
,
…
,
n
.
{\displaystyle x_{i}^{(k+1)}={\frac {1}{a_{ii}}}\left(b_{i}-\sum _{j\neq i}a_{ij}x_{j}^{(k)}\right),\quad i=1,2,\ldots ,n.}
xi(k+1) hesablanması x(k)-də özündən başqa hər bir elementin olmasını tələb edir.
Xətti bərabərlik sistemi
A
x
=
b
{\displaystyle Ax=b}
formasında və onun ilkin fərz edilən həlli
x
(
0
)
{\displaystyle x^{(0)}}
verilib
A
=
[
2
1
5
7
]
,
b
=
[
11
13
]
and
x
(
0
)
=
[
1
1
]
.
İstehsal üsulu
İstehsal üsulu (alm. Produktionsweise) — Marksizmə görə, məhsuldar qüvvələrin və onların şərtləndirdiyi istehsalat münasibətlərinin vəhdəti. İçtimai istehsal üsulları, bir tərəfdən — müvafiq istehsalat texnoloqiyasının tarixi tipinə görə (məhsuldar qüvvələr), o biri tərəfdən — istehsal və bölgü əsnasındakı istehsal şəraitinə və vasitələrinə olan hakim münasibətlərin müvafiq iqtisadi gerçəkləşdirilməsi tipinə görə(istehsalat münasibətləri) fərqlənirlər. Hakim istehsal üsulu ictimai-iqtisadi formasiyanın özülü(bazisi) sayılır.
Gömrük-tarif tənzimlənməsi
Gömrük-tarif tənzimlənməsi — gömrük sərhədindən keçirilən mallara tətbiq edilən və xarici iqtisadi fəaliyyətin mal nomenklaturasına uyğun olaraq sistemləşdirilmiş gömrük rüsumu dərəcələrinin məcmusudur. Malların idxalı və ixracı üzrə gömrük rüsumları gömrük tarifinə əsaslanır. Malların idxalı və ixracı ilə bağlı qanunvericilikdə nəzərdə tutulmuş digər tədbirlər bu malların tarif təsnifatına uyğun olaraq tətbiq olunur.
Gömrük rüsum normaları müəyyən olunarkən iki yanaşma əsas götürülür – fiskal yanaşma və tənzimləyici yanaşma. XIX əsrin sonları və XX əsrin əvvəllərində gömrük rüsum normalarının müəyyən olunmasında fiskal yanaşmaya üstünlük verilirdi və rüsumlar dövlət gəlirlərinin mühüm mənbəyi kimi baxılırdı.
XX əsrin ortalarından başlayaraq gömrük rüsum normalarının azalması meyli üstünlük təşkil etməyə, tənzimləyici yanaşma ön plana çıxmağa başladı. Belə şəraitdə gömrük rüsum normalarının mal qrupları və konkret məmulatlar üzrə differensasiyasına tələbat artdı.
Gömrük tarifi aşağıdakılar əsasında müəyyən edilir:
xarici iqtisadi fəaliyyətin mal nomenklaturası;
tamamilə və ya qismən xarici iqtisadi fəaliyyətin mal nomenklaturasına əsaslanan və malların ticarəti ilə bağlı tarif tədbirlərinin tətbiqi məqsədilə xüsusi sahələri tənzimləyən qanunvericilik aktları ilə müəyyən edilmiş digər nomenklatura;
xarici iqtisadi fəaliyyətin mal nomenklaturasının əhatə etdiyi mallara tətbiq olunması nəzərdə tutulan avtonom və ya konvensiya idxal gömrük rüsumları;
müəyyən ölkələrlə, yaxud beynəlxalq təşkilatlarla bağlanılmış beynəlxalq müqavilələrdə nəzərdə tutulmuş preferensial tarif tədbirləri;
müəyyən ölkələrə, yaxud beynəlxalq təşkilatın üzv ölkələrinə münasibətdə birtərəfli qaydada qəbul edilən preferensial tarif tədbirləri;
müəyyən mallar üzrə gömrük rüsumlarının azaldılmasını, yaxud gömrük rüsumlarından azadedilməni təmin edən tədbirlər; müəyyən malların xüsusiyyətləri, yaxud son istifadəsi ilə əlaqədar olaraq, bu Məcəllə və müvafiq qanunvericiliklə müəyyən edilmiş güzəştli tarif rejimi; kənd təsərrüfatını, ticarəti və başqa sahələri tənzimləyən qanunvericiliklə müəyyən edilmiş digər tarif tədbirləri.
Malların tarif təsnifatı gömrük rüsumları, vergilər, malların idxalı və ixracı üzrə qadağalar və məhdudiyyətlər barədə məlumat toplusundan ibarətdir. Gömrük orqanları gömrük rüsumlarının və qanunvericilikdə nəzərdə tutulmuş vergilərin tətbiqində malların tarif təsnifatından istifadə edirlər.

Qeyri-Elektrolitlər
Dielektriklər — elektrik cərəyanını keçirməyən maddələrdir. Dielektriklərin qaz, maye və bərk növləri var. Dielektriklər neytral atom və ya molekullardan təşkil olunmuşdur. Dielektriklərin iki növü vardır: polyar və qeyri-polyar. Onlar molekulların quruluşuna görə bir-birindən fərqlənirlər. Elektrik sahəsində dielektrikin bağlı yükləri əks istiqamətlərdə yerini dəyişir; dielektrik polyarlaşır. Polyarlaşmış dielektrik özü elektrik sahəsi yaradır. Bu sahə dielektrikin daxilində xarici elektrik sahəsini zəiflədir.
Dielektrikin polyarizasiyası-xarici elektrik sahəsində dielektrikin qarşı üzlərində əks işarəli bağlı elektrik yüklərinin yaranmasıdır.
Dielektrik nüfuzluğu-dielektrik daxilində sahə intensivliyinin vakuumdakı sahə intensivliyindən neçə dəfə kiçik olduğunu göstərən fiziki kəmiyyətdir: ε=E0/E. Dielektrik nüfuzluğu adsız kəmiyyətdir və maddənin növündən asılıdır.
Qeyri-adi
Qeyri-adi — nadir halda rast gəlinən, sistemə salınmamış, insanlarda təəccüb doğuran, təkrarlanmayan, ənənələri ya az, ya heç olmayan, tez-tez dəyişilən, rastlaşanda maraq doğuran, istisna, standartdan fərqlənən, qeyri-adiliyi ilə seçilən hal, vəziyyət, insan, situasiya və s.
Fəlsəfə
Filologiya
Adi
С.И.Ожегов. Словарь русского языка. Москва, изд. "Русский язык", стр.348.
